あの覚えにくい公式、実は仲良しだった!? ~数学・微分~

📘 あの覚えにくい公式、実は仲良しだった!?
こんにちは!横浜市戸塚区柏尾町の学習塾、フィロソフィア柏尾教室講師の中臺(なかだい)です。
本日は高校で習う「微分」という内容を、中学で覚えにくかった“あの公式”と一緒に、やさしくお話ししたいと思います!
それでは本日の主役に登場してもらいましょう〜!
半径rの球の表面積さんと体積さんです〜!
👉 球の表面積
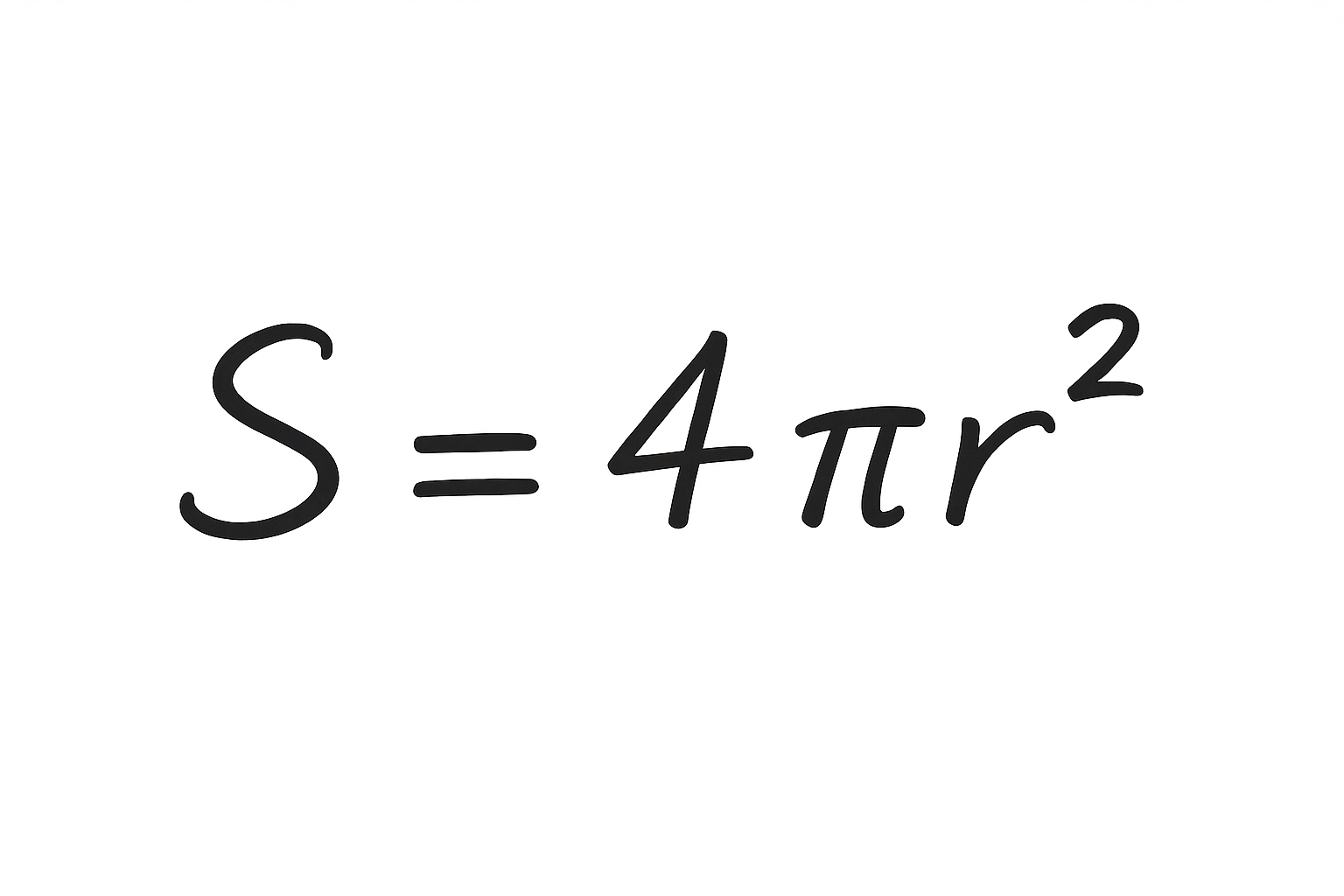
👉 球の体積
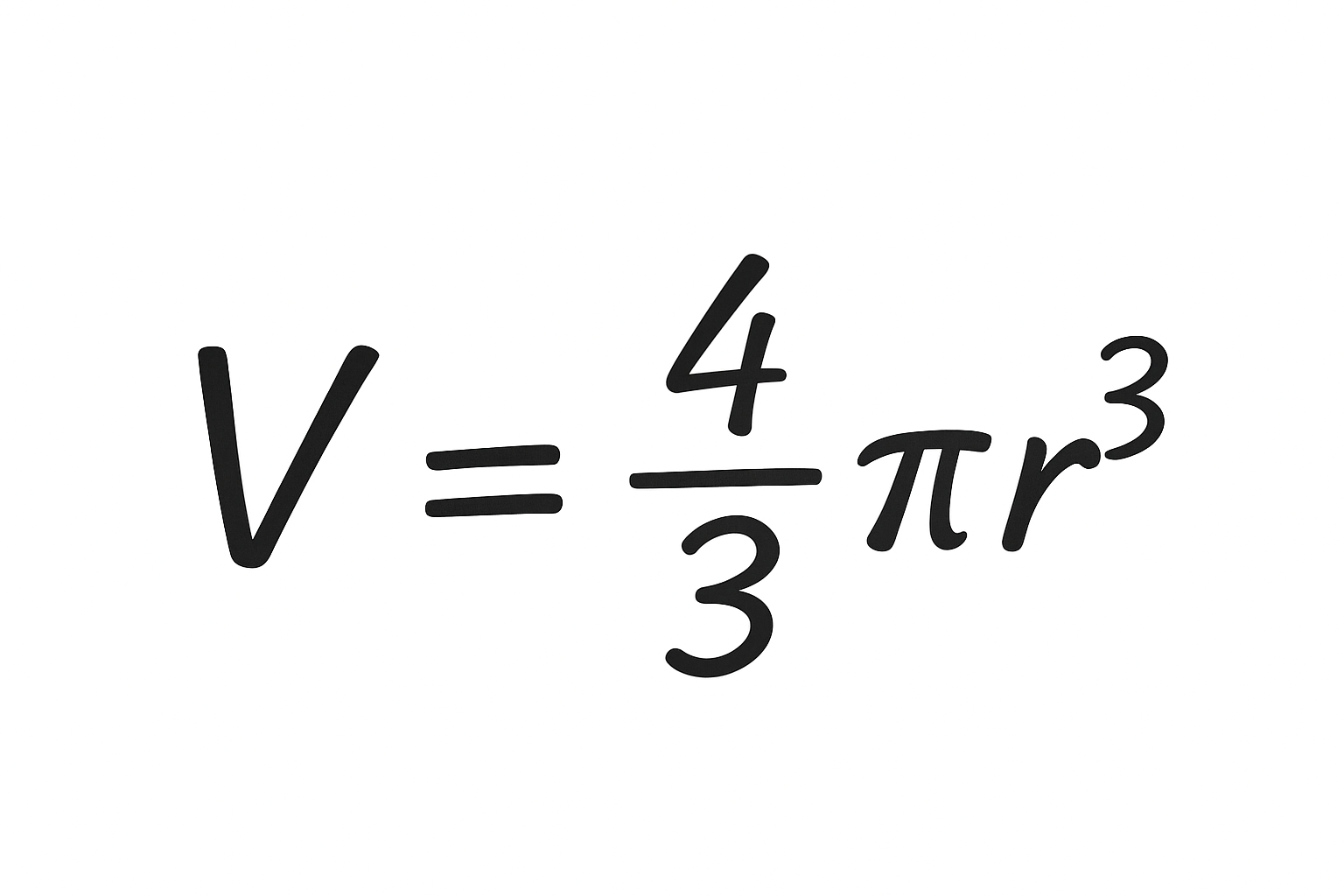
「数字は似てるけど、覚えにくいな〜」と感じた方、多いのではないでしょうか?
実はこの2つ、ただの暗記ではなく“微分”でつながっているんです!
🌀 「微分」ってなに?
微分というのは、簡単に言うと「変化のしかた」を調べる方法です。
たとえば、半径rの球をちょっとだけ大きくしたとき、
「体積はどのくらい増えるんだろう?」というのを調べるイメージです。
それを考えるのを「微分する」というのです。
そして、実は微分の計算のしかたはとってもシンプル。
Xⁿ を微分すると、n×xⁿ⁻¹ になる
つまり、指数を1つ下げて、その指数を前にかけるだけ!
たとえば、
X³ → 3X²
X² → 2X
という感じです。
✏️ 体積を微分してみよう
この方法を用いて、体積を微分してみましょう。
球の体積は、
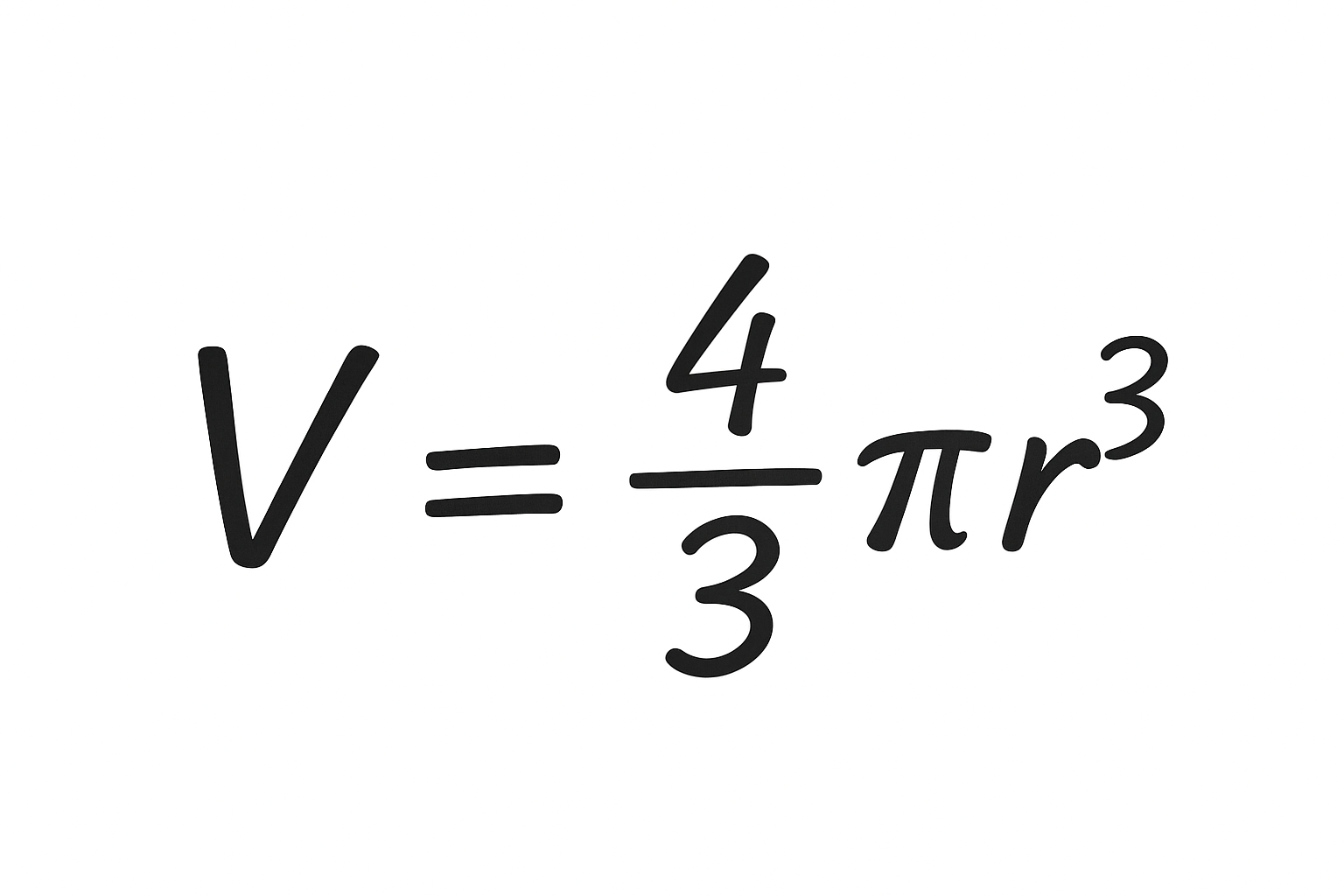
これをrで微分すると、
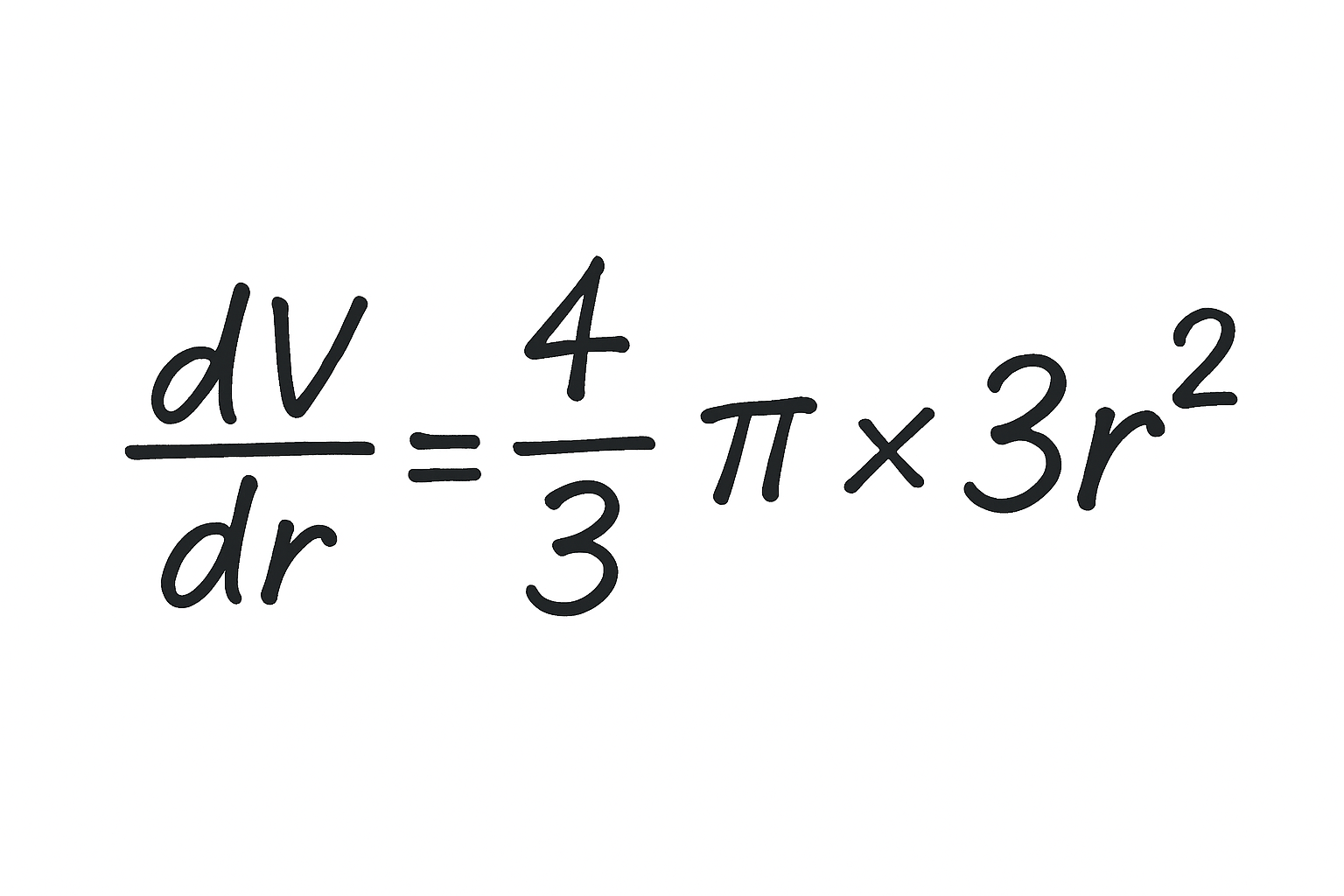
3が前に出て指数が1つ下がるので、
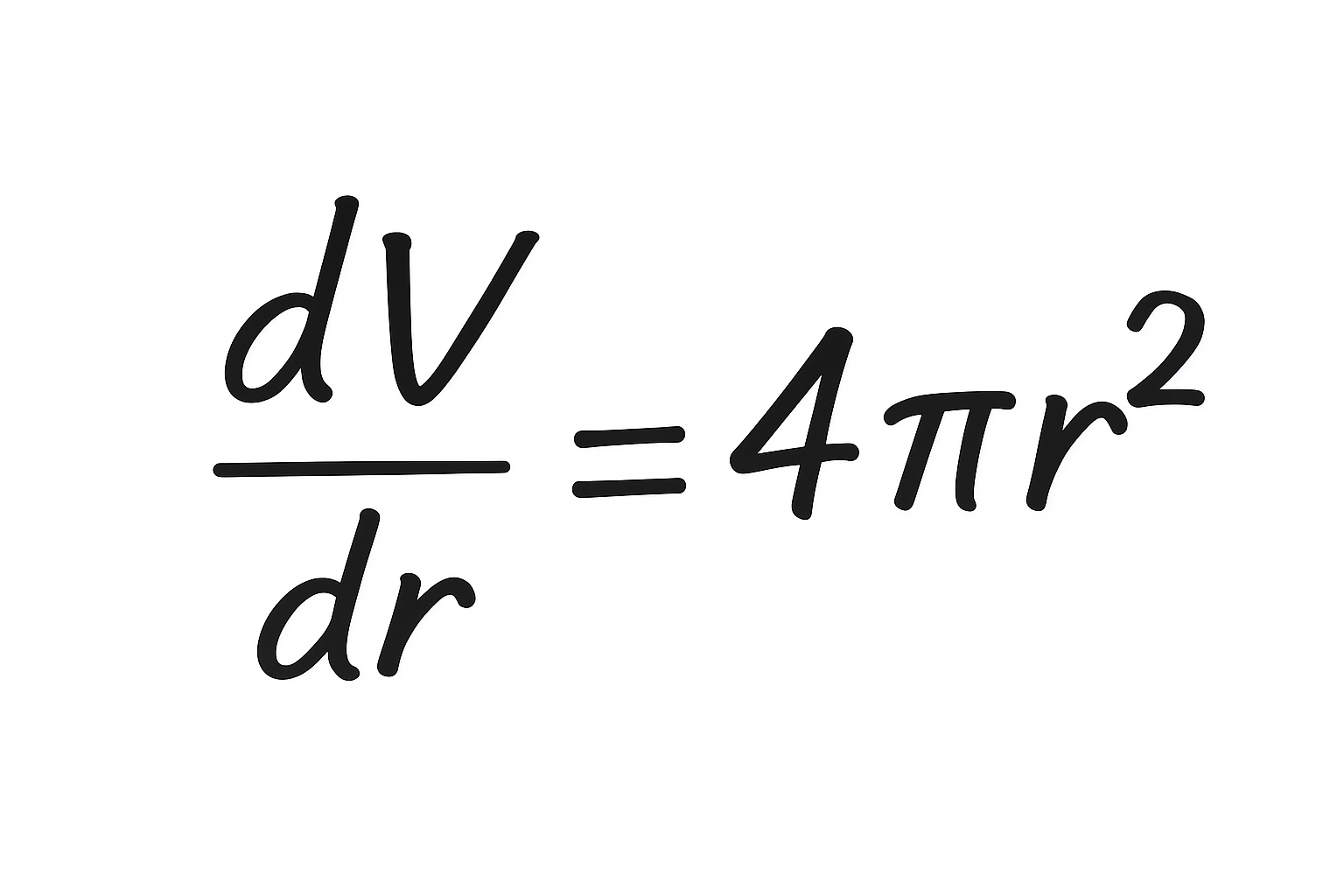
はい、出ました!!
これ、まさに表面積の公式です!👏
つまり「体積を微分すると表面積になる」ってわけなんです。
🌱 まとめ
私は高校生のときにこれを知って、「うわ〜すごい!」って感動しました。
中学で「なんで似てるんだろう、、、?」と思っていた疑問がスッキリした瞬間です。
数学って、暗記だけじゃなくて、“つながり”を見つけるとぐっと面白くなるんですよね!
そんな「わかる」「つながる」楽しさを一緒に体験できる授業を心がけています。
体験授業や面談も行っていますので、もし興味を持ってくださった方は、ぜひお気軽にお問い合わせくださいね☺️