【算数・数学】分数のわり算、なんで「逆数」にするの?

裏返すのはなぜ?
こんにちは!戸塚区柏尾町の学習塾、フィロソフィア柏尾教室講師の中臺(なかだい)です。
分数の計算って、足し算や引き算まではスムーズなのに、割り算になったとたん「逆数にしてかける」という急なルールが出てきますよね。
分母と分子を逆にして、かけ算する。
「どうして割るのに、かけるに変わるの?」
「逆数って結局なに?」
たしかに、ここでつまずくか、あるいはよくわからないままやっている方もけっこういらっしゃるんじゃないかと思います。
今日はそんな、謎多き分数のわり算を、イメージでわかりやすく整理していきましょう!
※このブログ内の「1/3」という表記は、「3分の1」の意味です。
➗ 「割る」って、そもそもどういうこと?
まずはじめに、「割る」の意味を思い出してみましょう。
6 ÷ 2 は「6を2ずつに分ける」または「2がいくつ分あるかを調べる」ということでしたね。
では、6 ÷ 1/2 のように割る数が分数になったらどうなるでしょうか?
「6を1/2ずつに分ける」と考えると、
6の中に1/2がいくつ入るかを数えることになります。
実際にやってみると、
6 ÷ 1/2 = 12
つまり、1/2が12個入るんです。
これは「6を2倍した」と同じ結果ですね。
つまり「割る1/2」という操作は「2倍する」と同じこと。
これが「逆数をかける」の第一歩なんです。
🍫 チョコバーを分けてみる
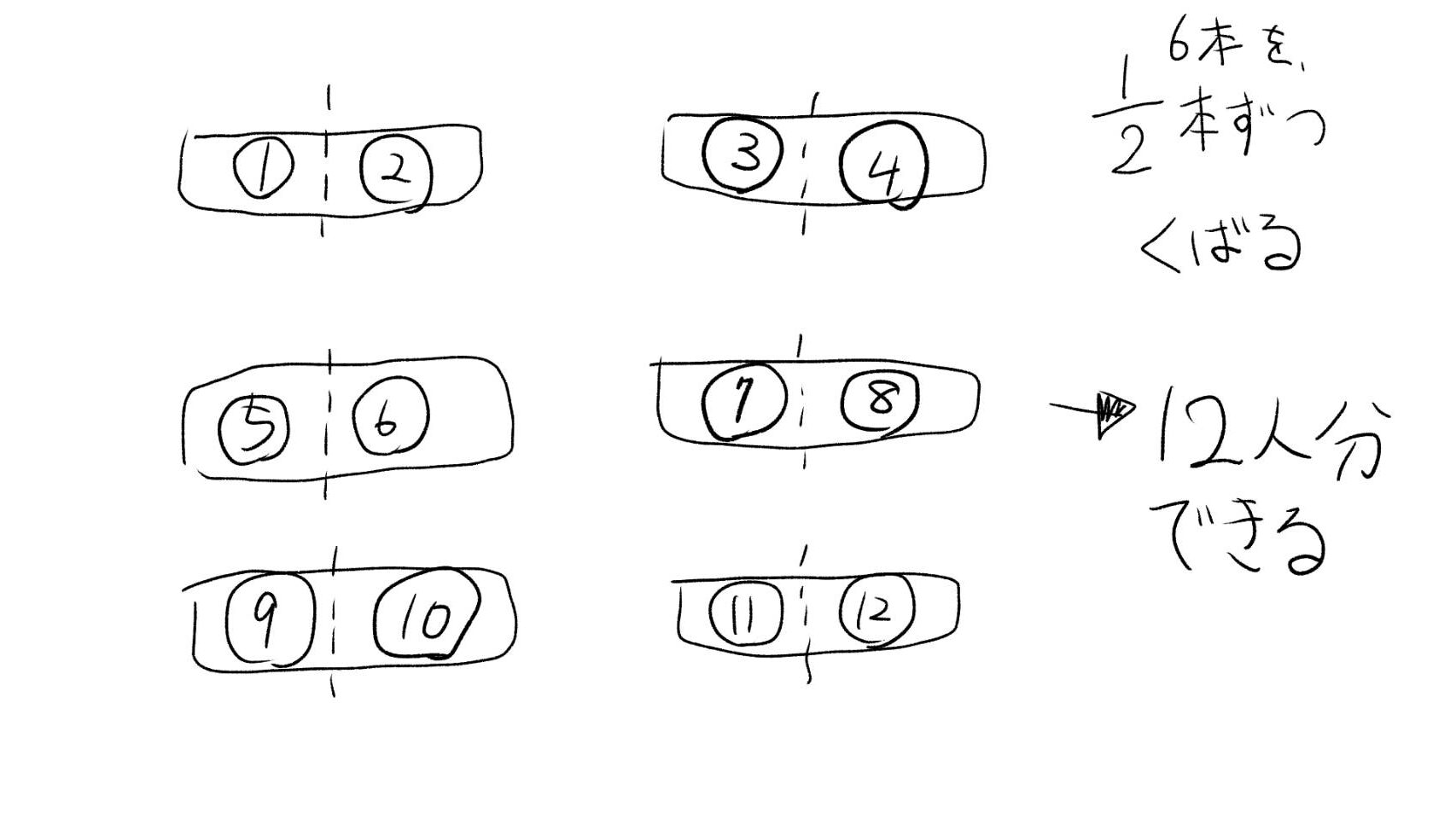
たとえば、長いチョコバーを6本並べてみましょう。
これを「1/2本ずつ」に分けていくと、1本のチョコが2つに分かれるので、全部で12人に分けられます。
つまり、
6本 ÷ 1/2本 = 12人分。
「6 ÷ 1/2 = 6 × 2」
図で見るととっても納得できますね。
🔁 なぜ「逆数をかける」と同じになるの?
「÷1/2」は「×2」と同じことを意味していました。
この関係はもちろん、「2」じゃなくても同じです。
たとえば「÷1/3」は「×3」、「÷1/4」は「×4」。
つまり、「分母が小さいほどたくさんに分ける」=結果が大きくなるのです。
このときの「3」や「4」にあたるのが、逆数です。
逆数とは「分母と分子をひっくり返した数」のことで、割ることの代わりに「いくつ分あるか」を表してくれる数なんです。
🧠 つまり、「割る」とは?
まとめると、こうなります。
割るとは「いくつ分あるか」を調べること。
割る数が分数のときは、「その分数がいくつ分入るか」を考える。
「割る1/2」は「2倍する」と同じ。
だから、分数で割る=逆数をかけるというルールになる。
覚えるだけだと不思議なルールですが、意味で考えるとすっきりつながりますね!
こうやって理屈を理解しておくと、忘れにくくなります。
🎂 仕上げに、ケーキを分けてみる
この逆数の理屈を理解していると、生活の中でも使えます!
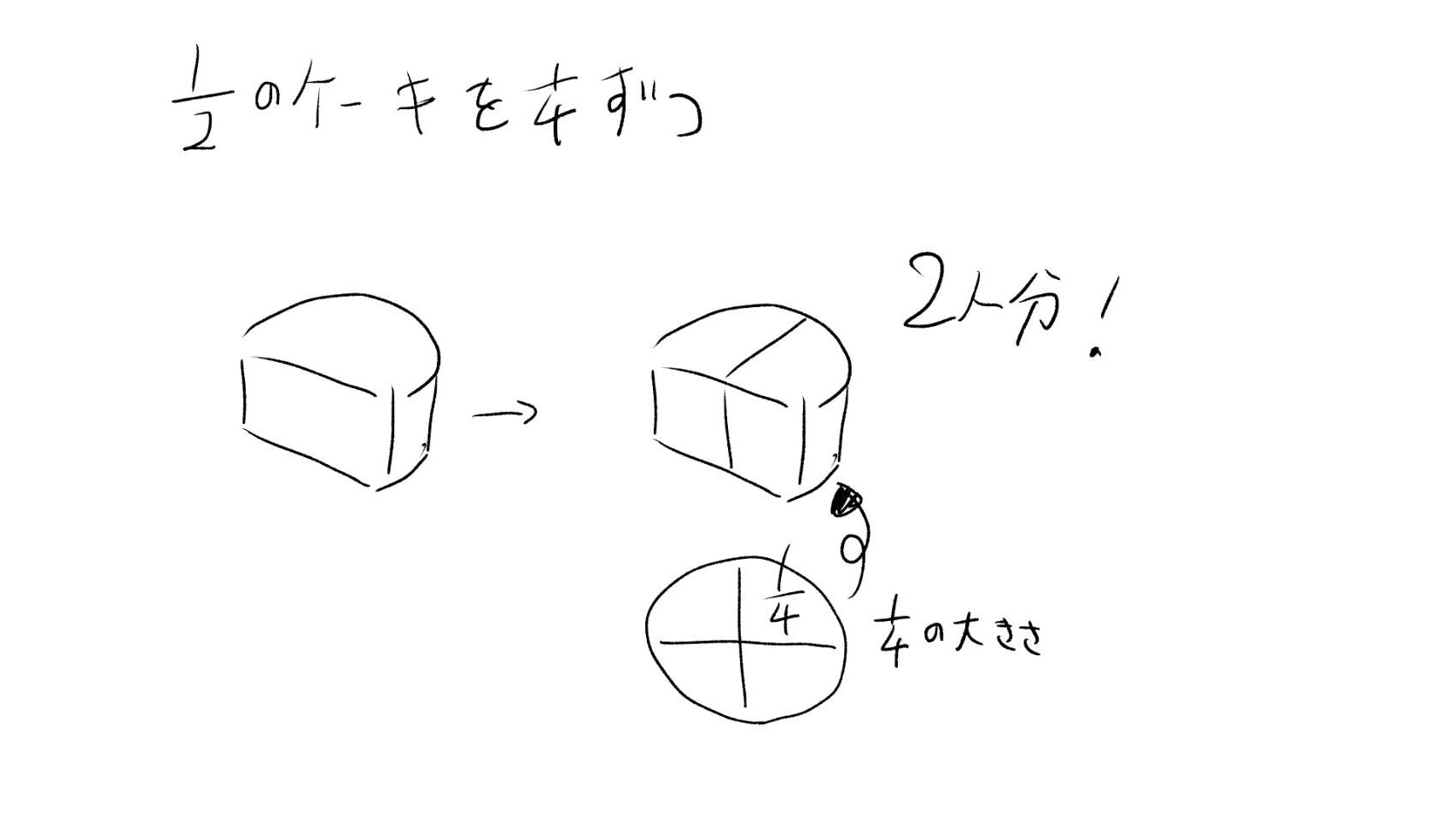
ケーキを1/2個持っていて、それを1/4個ずつ分けたいとき、いくつに分けられるでしょう?
1/2 ÷ 1/4
= 1/2 × 4 = 2
つまり、2人分になります。
※同じように、1mの板チョコを1/5mずつ切るときは、
1 ÷ 1/5
= 1 × 5 = 5
で、5本に切れます。1mのは、あんまり見たことないかもしれませんが。
🔥これで、ケンカにならずに分けられます。🔥
「いくつ分できるか」という考えかたで見れば、分数のわり算もぐっと身近に感じられますね。
ということで、今日は「分数のわり算=逆数をかける」の理由を、イラストを使って考えてみました。
目で見えるかたちにすると、ぐっとわかりやすくなりますよね。
(ちなみに、この広い意味で「見えるようにする」というのはとても普遍的、つまりどこでもなんにでも通用するやりかたで、算数や数学にかぎらず、いろんなところで役立つテクニックです。興味のある方は、ぜひ下記の「見える化」について触れている記事も読んでみてください。)
👉ブログ記事『【勉強法】「続けられる環境」をつくる』はこちら
分数のわり算の仕組みや面白さが少しでも伝わっていたらいいなと思います!
それではまた!
当塾では、身近なものを例にとって考えたり、直感的に理解できるように図解したりしながら、楽しく知識を定着させる授業を行っております。
完全個別指導や少人数制の授業など、一人ひとりの個性やご希望に合わせたプランをご用意しておりますので、安心して受けていただけます。
体験授業や面談も行っております。
ご相談だけでもかまいません。下記フォームより、お気軽にお問い合わせください!
***
▶ お問い合わせフォームはこちら
▶ HPトップはこちら